On this page, I will list some research projects I have done with (usually) undergraduate students, or that I would be interested in doing, and give brief descriptions. If you are interested in learning more, or doing research in general, please talk with me!
Generating Weakly Complete Sequences
I have a rule which I use to make sequences of positive integers with the following property:
there is some number \(N \) such that every integer larger than \( N \) can be written
as a sum of terms in the sequence. If you use this rule to generate sequences, then the sequences
you get seem to have some very nice patterns. For example, if you want to use my rule to make a sequence starting with the numbers 1 and 5 (you can choose any numbers you want to start the sequence before using the rule), then the sequence you end up with is
\[ 1, 5, 7, 9, 11, 29, 31, 89, 91, 269, 271, 809, 811, 2429, 2431, \ldots. \]
What you might notice here is that after the first few terms, the numbers come in pairs. You have 9 and 11, then 29 and 31, then 89 and 91, and so on. Even nicer, you can find a formula for the pairs. The numbers in each pair are \( 10 \cdot 3^k \pm 1\), where \( k \) is a positive integer. The goal of the projects I have done in this area (and also for future projects!) is to try to prove that patterns like this always exist.
Students:
Michael Paul, Summer 2008 Hauber project
Alyson Fox, Summer 2009 Hauber project
Kyle Leblanc, Summer 2020 Hauber project
Publications:
M. Knapp and M. Paul, "On weakly complete sequences formed by the greedy algorithm" Integers 12 (2012) A4, 18pp.
A. Fox and M. Knapp, "A note on weakly complete sequenes." Journal of Integer Sequences 16 (2013), no. 6, Article 13.6.2, 14pp.
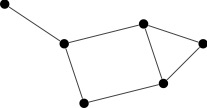
Bounded Chromatic Polynomials
Chromatic polynomials are a fundamental concept in graph theory. In this context, a graph means a set of dots (called vertices), some of which may be connected by lines (called edges). For example, the graph below has 6 vertices and 7 edges.

Exact Values of the Function \( \Gamma^*(k) \)
In linear algebra, one of the first "big" theorems we learn is that if we have a homogeneous system of equations
\[ \begin{array}{cccccccc}
a_{11}x_1 & + & \cdots & + & a_{1s}x_s & = & 0\\
\vdots & & & & \vdots & & \vdots \\
a_{R1}x_1 & + & \cdots & + & a_{Rs}x_s & = & 0,
\end{array} \]
with more variables than equations (so \(s > R\)), then the system has a nontrivial solution, no matter what the coefficients are. Even better, it's not too hard to see (although this is usually not taught in linear algebra) that if the coefficients are all integers, then we can find a solution where the variables are also all integers. I am interested in similar problems where you put exponents on the variables. So for a single equation, I am interested in equations that look like
\[ a_1x_1^k + a_2x_2^k + \cdots + a_sx_s^k = 0. \]
It turns out that (with some small restrictions), equations like this have a similar property. If there are "enough" variables, and the coefficients are all integers, then there is guaranteed to be a nontrivial solution where the variables are all integers, no matter what the (integer) coefficients are. I am interested in finding out how many variables is "enough." If we know the value of \(k\), how many variables do we need to guarantee that there are solutions?
Actually, this problem can be quite hard, so I'm interested in a variant that seems more complicated at first, but actually turns out to be a bit easier. Instead of showing that we can make the polynomial be equal to 0, I try to show that we can make the polynomial be divisible by any integer we want. In this variant, we want to show that there are integers so that \( a_1x_1^k + \cdots + a_sx_s^k \) is divisible by 2, there are (possibly different) integers so that \( a_1x_1^k + \cdots + a_sx_s^k \) is divisible by 3, and so on. There are a few questions that we can ask here.
The Coin Flip Sequence Game
Suppose that you and I play the following game. Each of us picks a sequence of three flips of a coin, where each flip is either \(H\) (heads) or \(T\) (tails). For example, suppose you pick the sequence \(HTH\) and I pick the sequence \(TTT\). Then we repeatedly flip a coin, and the winner of the game is whoever's sequence comes up first in three consecutive flips. For example, if we start flipping the coin and get the sequence \( HHTTHTTHTH\), then you win because we have had three consecutive flips of \(HTH\) and we have not had three consecutive flips of \(TTT\). The really interesting thing about this is that it's not a fair game! Even though it's true that if you flip a coin 3 times, all sequences come up with equal probability, it is not true that every sequence has an equal probability of coming up first when we flip a coin repeatedly. In fact, it turns out that \(HTH\) will beat \(TTT\) about 58% of the time. I understand the game very well for sequences of 3 flips, but have never studied sequences of more than 3 flips. I think there are several interesting questions that could be asked here.
Rational Values of Generating Functions
The Fibonacci sequence is the well-known sequence of numbers
\[ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, \ldots, \]
in which the first two numbers are defined to be 0 and 1, and every other number in the sequence is found by adding the two numbers before it. The generating function for the Fibonacci sequence is the function \(F(x)\) defined by the infinite power series
\[ F(x) = 0 + 1x + 1x^2 + 2x^3 + 3x^4 + 5x^5 + 8x^6 + 13x^7 + \cdots \; = \; \frac{x}{1-x-x^2}, \]
where the coefficients are the consecutive Fibonacci numbers. (The fact that this series equals \( x/(1-x-x^2) \) is not obvious.) An interesting question which was asked a few years ago is: what rational numbers \(x\) make the value of \(F(x)\) an integer? For example, we have
\[ F(2/3) = \frac{2/3}{1 - (2/3) - (2/3)^2} = -6. \]
This specific problem has been solved, but it can be the jumping-off point for several other interesting problems.
Generalizing a Grid-Cutting Problem
A problem on a mock AMC-10 high school contest published on the Art of Problem Solving website asked the following question. Suppose you have a \( 3 \times 3\) grid of boxes, as shown below.


Variations on the Chopsticks Finger Game
Chopsticks is a (typically) two player game in which each player starts by holding out one finger on each hand. On each player's turn he "taps" one of the hands of the opposing player, and the number of fingers held out on the "tapped" hand increases by the number of fingers on the "tapping" hand. The objective of the game is to eliminate both of the opponent's hands by causing them to have exactly five fingers out. The goal of this project was to study variations of this game - for example, pretending that people have 6 fingers on each hand, or starting with a different configuration of fingers - and determine which player has a winning strategy.
Students:
Colin Habig, Summer 2017 Hauber project